
Fuente: bbc.com
Autora: Margarita Rodríguez
Emmy Noether Amalie (Baviera, Alemania, 23 de marzo de 1882 – Pensilvania, Estados Unidos, 14 de abril de 1935) fue una matemática alemana, especialista en la teoría de invariantes y conocida por sus contribuciones de fundamental importancia en los campos de la física teórica y el álgebra abstracta. Considerada por David Hilbert, Albert Einstein y otros personajes como la mujer más importante en la historia de la matemática, revolucionó la teoría de anillos, teoría de cuerpos y la de K-álgebras. En física, el teorema de Noether explica la conexión fundamental entre la simetría en física y las leyes de conservación.
Cuando Emmy Noether quiso estudiar matemáticas, no estaba permitido que las mujeres se inscribieran en la universidad. Años después, cuando consiguió que le dieran permiso para dar clases a estudiantes universitarios, no recibió salario. Aun así, para Albert Einstein,
«la señorita Noether fue el genio matemático creativo más importante que haya existido desde que comenzó la educación superior para las mujeres».
Se la considera la madre del álgebra moderna con sus teorías sobre anillos y cuerpos, pero su aporte a la ciencia no se restringe a las matemáticas. Su trabajo es fundamental para entender la teoría de la relatividad. Y tampoco se limita a ella.
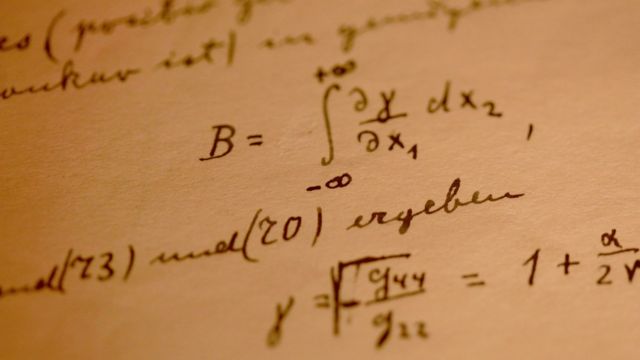
GETTY IMAGES. Un detalle de los apuntes de Albert Einstein sobre la Teoría General de la Relatividad.
Noether es clave para comprender todas las teorías de la física.
«Al conocer su historia te preguntas: ¿qué otras contribuciones hubiese hecho una persona con ese tipo de genio matemático si todas las puertas hubiesen estado abiertas para ella desde el primer día?», le dice a BBC Mundo Mayly Sánchez, profesora de Física del departamento de Física y Astronomía de la Universidad del Estado de Iowa, en Estados Unidos.
Sin salario
Nació en 1882 y su padre, el matemático Max Noether, enseñaba en la Universidad de Erlangen, en Baviera.
 El claustro de esa casa de estudios había dicho que permitir que las mujeres se registraran «derrocaría todo el orden académico«.
El claustro de esa casa de estudios había dicho que permitir que las mujeres se registraran «derrocaría todo el orden académico«.Sin embargo, dos años después -indica la Sociedad Estadounidense de Física (APS, por sus siglas en inglés: American Physical Society)- Noether fue una de las dos estudiantes a la que se le permitió inscribirse en esa universidad.
Pero no con los mismos derechos que el resto de estudiantes. Sólo se le permitía entrar como oyente a las clases y eso si los profesores daban la autorización expresa de que podía entrar al aula.
«Pero eso fue suficiente para que pasara el examen de graduación en 1903 y para que calificara a un título equivalente al de una licenciatura», indica Michael Lucibella, autor de la biografía sobre Noether publicada por APS.
«Pasó el año siguiente estudiando en la Universidad de Gotinga, pero regresó a Erlangen cuando la universidad finalmente revocó las restricciones contra las estudiantes y terminó su disertación sobre invariantes para las formas biquadráticas ternarias en 1907», señala el escritor.
Pese a que la universidad dio un paso adelante para permitir a mujeres estudiantes, continuaba excluyendo a las mujeres de tener posiciones en la facultad. «Noether enseñó en Erlangen por los siguientes siete años sin salario, en algunas ocasiones reemplazando a su padre», indica Lucibella.
«Somos una universidad, no un sauna»
En 1915, el gran matemático alemán David Hilbert trató de llevarla a la Universidad de Gotinga, pero recibió el rechazo de sus colegas en el departamento de matemáticas.
«¿Qué pensarán nuestros soldados cuando regresen a la universidad y encuentren que se les pedirá que aprendan de una mujer?», un profesor se quejó de la propuesta.
A lo que Hilbert respondió: «No veo por qué el sexo de los candidatos sea un argumento contra su admisión. Somos una universidad, no un sauna».
Noether tuvo que dar clases bajo el nombre de Hilbert por los siguientes cuatro años y sin pago alguno.
Lucibella explica que la esperanza de Hilbert de contar con la matemática en la Universidad de Gotinga era que su conocimiento y experiencia sobre «la teoría invariante -los números que se mantienen constantes incluso aunque sean manipulados de diferentes maneras- pudiera ser llevada a la incipiente teoría general de la relatividad de Albert Einstein, que parecía violar la (ley) de la conservación de energía».
El teorema de Noether
Noether desarrolló un teorema que es clave para entender la física de partículas elementales y la teoría cuántica de campos. En pocas palabras, «para comprender toda la física más sofisticada», le dice a BBC Mundo Manuel Lozano Leyva, catedrático de Física Atómica y Nuclear de la Universidad de Sevilla.

AFP/GETTY IMAGES. Una copa de vino para entender un teorema clave en la física.
«Cuando Einstein vio el trabajo de Noether sobre las invariantes, le escribió a Hilbert: ‘Estoy impresionado de que esas cosas puedan ser entendidas de una manera tan general. La vieja guardia de Gotinga debería aprender algunas lecciones de la señorita Noether. Se ve que sabe de lo suyo'», indica la biografía de APS.
«El teorema conceptualmente es muy sencillo y matemáticamente muy complicado. Se trata de relacionar la simetría con las cantidades conservadas», dice el profesor de Física Manuel Lozano Leyva.
«¿Qué es una simetría?», empieza.»Imagínese que tengo una copa de vino en la mano y le digo que cierre los ojos. Mientras los tiene cerrados, giro la copa en su eje y después le digo que los abra. Seguramente no se dará cuenta si la copa se ha movido o no. Pero si el giro que hago es perpendicular a ese eje, es decir, le doy la vuelta a la copa, y le digo que abra los ojos, sí se dará cuenta que ha habido una transformación, que le ha pasado algo a la copa. Eso significa que la copa es simétrica con respecto a las rotaciones en relación a un eje y no es simétrica respecto a las rotaciones en otro eje«.
Es un teorema sumamente elegante, trae la belleza de un concepto de simetría a lo que son los principios de la física. «Ahora piense», señala el profesor, «en cantidades físicas que todo el mundo conoce como lo es la energía, que ni se crea ni se destruye, sino que se transforma. Eso se llama una cantidad conservada».
«Lo que hizo Emmy Noether fue fundamentalmente relacionar la simetría de un sistema con las cantidades físicas que se conservan y esas cantidades son una herramienta fundamental a la hora de plantear problemas y de resolverlos en física».
Y eso afecta a todos los sistemas físicos, desde el sistema planetario hasta un cristal, los metales. «¡Todo!».
¨El teorema más bello del mundo¨
El teorema creado por la científica alemana ha recibido un sinnúmero de adjetivos y no precisamente fríos.

La profesora Sánchez explicándoles el teorema de Noether a sus alumnos en Estados Unidos.
«Lo llaman el teorema más bello del mundo, pero no es solo que sea hermoso por las cuestiones de la simetría sino que es de una potencia matemática tremenda y de una potencia de cálculo fantástica», indica Lozano. «Mis estudiantes quedaban maravillados cuando se los enseñaba porque, aunque sea matemáticamente difícil de formular, las consecuencias son muy grandes«.
«A esta mujer le debemos mucho todos los físicos«, señala el profesor desde España. Y esa opinión la comparte la profesora Sánchez desde Estados Unidos. «Noether es una de esas figuras en la historia de la física que se te esconden y después la descubres«, cuenta. «Cuando aprendí el teorema por primera vez, me enamoré del concepto. Mi profesor nos dio una clase bellísima de cómo este era uno de los principios más elegantes de la física y, ahora, que enseño la misma materia en el pregrado, todavía me emociono cuando doy esa clase. Es uno de los puntos donde la física y la matemática se conectan de una manera muy bonita». «Lo que no me dijo el profesor ese día es que el teorema de Noether estaba escrito por Emmy Noether. Nunca me dijo que era una mujer y solo años más tarde, en mi doctorado, descubrí que había sido una mujer la que lo concibió».
¨Los chicos de Noether¨
Tras el fin de la Primera Guerra Mundial, hubo algunos avances en materia de los derechos de las mujeres en Alemania.
«Noether recibió un pequeño salario en la Universidad de Gotinga en 1923, sin embargo, nunca se le otorgó el rango de profesora titular«. La mayoría de los estudiantes de la matemática eran hombres. Se les conocía como «Los chicos de Noether», indica la Sociedad Estadounidense de Física.
Con el surgimiento del Nazismo en Alemania, Noether tuvo que abandonar la vida académica en su país debido a la puesta en vigencia de una ley que sacaba a los judíos de posiciones gubernamentales y universitarias. Noether fue despedida de la casa de estudios de Gotinga. Inicialmente recibió a los estudiantes en su casa, pero finalmente fue forzada a abandonar Alemania, junto a muchos otros académicos judíos. Se fue a Estados Unidos, en donde continuó con su vida académica en el Colegio Bryn Mawr de Princeton y en el Instituto de Estudios Avanzados de esa ciudad.
En 1935, le detectaron un tumor en la pelvis. Fue operada y aunque la intervención fue un éxito, una serie de complicaciones la llevaron a la muerte cuatro días después.
Tenía 53 años.














